1. 확률변수와 확률분포
-확률변수:무작위 실험을 했을때, 특정 확률로 발생하는 결과를 수치적 값으로 표현한 변수이다.
-이산확률변수: 랜덤변수는 보통 불연속적인 이산값인 경우가 많은데, 이를 이산확률변수라 한다. 이산적인 확률변수를 갖는 확률 분포로는 베르누이분포와 멀티눌리 분포가 있는데, 베르투이 분포는 0과 1의 값만 가질 수 있고, 멀티눌리 확률분포는 여러개의 이산값을 가질 수 있다.
-연속확률변수: 연속적인 값을 다루는 확률변수로, 확률 질량 함수대신 확률 밀도 함수를 통해 정의할 수 있다. 정규분포라고 불리는 가우시안 분포함수가 그 예이다.
-결합확률: 2개 이상의 사건이 동시에 일어날 확률을 말하며, 독립사건인 경우 두 확률의 곱으로 표현된다. P(A,B)=P(A)P(b)
-조건부확률: 하나의 확률 변수가 주어졌을 때 다른 확률 변수에 대한 확률 분포이다. P(A,B)=P(A|B)*P(B)
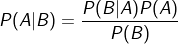
-주변확률분포: 2개 이상의 결합확률분포가 있을때, 하나의 확률변수에 대해서 적분을 수행한 결과를 말한다.

2. 기댓값과 샘플링
-기댓값: 보상과 그 보상을 받을 확률을 곱한 값의 총합이다. 즉, 특정함수에 대한 P(x) 분포에 따른 가중평균이라고 할 수 있다.
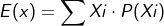
-몬테카를로 샘플링: 랜덤성질을 이용하여 임의의 함수 적분을 근사하는 방법이다. 밑의 식처럼 K번 샘플링한 값을 균등분포인 것처럼 다루어 가중평균 대신 단순한 산술 평균을 취한다.
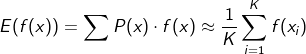
3. MLE
최대 가능도 추정(Maximum Likelihood Estimation)은 모수적인 데이터 밀도 추정방법으로 , 파라미터

위의 가능도에 로그를 취하여 곱을 합으로 표현할 수도 있다. 로그를 취하면 언더플로현상을 방지하고, 곱셈연산이 덧셈연산으로 바뀌어 더 빨라진다는 이점이 있다. 로그가능도값을 최대화하거나 로그가능도에 -1을 곱한 NLL값을 최소화하는 방법을 이용한다.

딥러닝에 쓰이는 신경망도 확률분포함수이기 때문에 신경망 가중치 파라미터 θ가 훈련데이터를 잘 설명하도록 경사하강법(gradient descent)을 통해 MLE을 수행하여 학습을 진행하게 된다.
4. 정보량과 엔트로피
-정보량: 불확실성을 나타내며, 정보량이 높을수록 어떤 일이 일어날 확률이 낮은 것을 뜻한다.

-엔트로피: 정보량의 평균(기댓값)을 나타낸다. 분포의 대략적인 모양을 알 수있으며, 엔트로피가 작을수록 분포는 뾰족한 모양을 갖는다. 즉, 확률분포가 뾰족할수록 특정값에 대한 확률이 높다는 뜻이다.
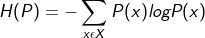
-교차 엔트로피: 분포함수 P에서 샘플링한 x를 통해 분포함수 Q의 평균정보량을 나타낸 것이다. 즉, 분포 P를 사용하여 대상 분포 Q의 엔트로피를 측정하는 것이다. -log값을 취했기 때문에 분포함수들이 비슷한 모양일수록 작은값을 가진다. 즉, 분류문제에서 교차엔트로피 손실함수를 최소가 되도록 경사하강법을 통해 신경망을 훈련하는 것이다. 여기서 중요한점은 앞서말했던 NLL을 최소화하는 과정과 교차엔트로피를 최소화하는 과정은 동일하다. 하지만 이 모든것은 확률 값을 얻을 수 있는 이산 확률 분포에만 적용이 된다. 연속확률 분포는 확률 값을 구할 수 없기 때문에, 신경망의 출력값이 가우시안 분포를 따른다는 가정을 하면 MSE를 통해 근사할 수 있게 된다.
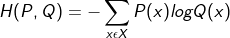
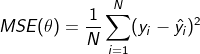
※본 게시물은 「김기현의 자연어처리 딥러닝캠프-파이토치편」을 참고하여 작성되었습니다.
'NLP' 카테고리의 다른 글
| 6. 단어 임베딩 (0) | 2021.07.21 |
|---|---|
| 5. 자연어의 중의성을 해결하는 법 (0) | 2021.07.21 |
| 4. 전처리 (0) | 2021.07.19 |
| 3. 파이토치 기초문법 (0) | 2021.07.13 |
| 1. 자연어 처리란? (0) | 2021.07.13 |